
'신호처리 > DSP 공부 필기' 카테고리의 다른 글
| [DSP 정리] # 6. Z-transform (0) | 2023.11.15 |
|---|---|
| [DSP 정리] # 5. Discrete-Time System (0) | 2023.11.15 |
| [DSP 정리] # 4. Discrete-Time Signal (0) | 2023.11.15 |
| [DSP 정리] # 2. 신호의 분류 및 특성 (0) | 2023.11.15 |
| [DSP 정리] # 1. 개요 (0) | 2023.11.15 |

| [DSP 정리] # 6. Z-transform (0) | 2023.11.15 |
|---|---|
| [DSP 정리] # 5. Discrete-Time System (0) | 2023.11.15 |
| [DSP 정리] # 4. Discrete-Time Signal (0) | 2023.11.15 |
| [DSP 정리] # 2. 신호의 분류 및 특성 (0) | 2023.11.15 |
| [DSP 정리] # 1. 개요 (0) | 2023.11.15 |




| [DSP 정리] # 6. Z-transform (0) | 2023.11.15 |
|---|---|
| [DSP 정리] # 5. Discrete-Time System (0) | 2023.11.15 |
| [DSP 정리] # 4. Discrete-Time Signal (0) | 2023.11.15 |
| [DSP 정리] # 3. Quantization (0) | 2023.11.15 |
| [DSP 정리] # 1. 개요 (0) | 2023.11.15 |
한양대학교 유경렬 교수님의 [디지털 신호 처리] 2011년도 강의 녹화본을 보고 정리한 내용입니다.

| [DSP 정리] # 6. Z-transform (0) | 2023.11.15 |
|---|---|
| [DSP 정리] # 5. Discrete-Time System (0) | 2023.11.15 |
| [DSP 정리] # 4. Discrete-Time Signal (0) | 2023.11.15 |
| [DSP 정리] # 3. Quantization (0) | 2023.11.15 |
| [DSP 정리] # 2. 신호의 분류 및 특성 (0) | 2023.11.15 |
electronic audio signal을 처리할 때, pre-emphasis 과정(transmitter에서 수행)에서 전체 frequency 대역 내에서 보통 높은 frequency 대역의 magnitude를 낮은 frequency 대역의 magnitude에 대해 상대적으로 증가시킨다. 이후 de-emphsis 과정(receiver에서 수행) 에서 recording media의 attenuation distortion이나 saturation등의 부작용을 최소화하여 SNR(signal-to-noise ratio)을 향상시킨다. 이러한 전체 시스템을 Emphasis하고 한다.
예측 가능한 noise를 미리 방지하는 것으로, 사전에 가장 민감한 frequency 대역에 distortion을 주는 것이다. 이렇게 하면 noise가 있는 케이블 전송, 테이프 녹음 등의 과정 후에 해당 frequency 대역에서 더 많은 정보를 복원할 수 있다.

Pre-emphasis으로 인해 발생한 distortion을 제거하는 과정(인위적으로 증폭했던 부분을 무표화함)이다. De-emphasis 과정을 통해서 output이 input을 정확하게 reproduct 할 수 있게 된다.

| 윈도우에서 AWS 설치 및 데이터셋 다운로드 (1) | 2024.12.13 |
|---|---|
| [DSP] CTFT와 DTFT의 관계 (0) | 2024.01.04 |
| [Sampling] Upsampling (0) | 2023.11.16 |
| Noise Pattern (0) | 2023.11.10 |
1. Gaussian Noise (White Noise) : 정규분포를 따르는 고정 잡음 유형
2. White Noise : 특정 frequency 대역에서 동일한 intensity를 갖는 random signal
3. Background Noise : target으로 하는 소리 외의 주변에서 발생하는 모든 소리
4. Brownian Noise (red noise) : brownian motion(액체/기체에서 나타나는 입자의 random motion)에 의해 생성되는 signal noise. 무작위한 변동을 가지면서도 시간이 지남에 따라 어느 정도의 bias 또는 drift를 나타냄.



1. Impulse Noise : 원치 않은 순간적인(impulse) 소리를 포함하는 noise로, 일반적으로 전자기 간섭, 디스크 긁힘, 총격, 폭발, 디지털 동기화 문제로 인해 발생
2. Transient Noise : 문닫는 소리, 자동차 경적 소리 등, 일상에서 짧게 발생되는 noise들
3. Reverberation : 반향은 주변 환경 요소에 계속 반사되면서 시간에 따라 변화하기 때문에 non-stationary noise로 여겨질 수 있음
4. Pink Noise : power spectrum의 밀도가 신호의 frequency에 역비례(1/f)하는 진동수 스펙트럼이 있는 signal. pink noise의 각 옥타브 주기는 동일한 양의 노이즈 에너지를 전달함. (생물학계에서 가장 흔한 신호들 중 하나라고 함.)

| 윈도우에서 AWS 설치 및 데이터셋 다운로드 (1) | 2024.12.13 |
|---|---|
| [DSP] CTFT와 DTFT의 관계 (0) | 2024.01.04 |
| [Sampling] Upsampling (0) | 2023.11.16 |
| [Emphasis] Pre-emphasis 와 De-emphasis (0) | 2023.11.10 |
STFT는 특정 짧은 시간 구간을 windowing을 통해 추출해내고 해당 구간 동안에 DFT를 하여 연산을 수행한다.
이때 windowing은 signal을 window와 time domain에서 multiplication을 시키는 과정이다. time domain에서의 multiplication 연산은 frequency domain에서는 convolution 연산과 같다.
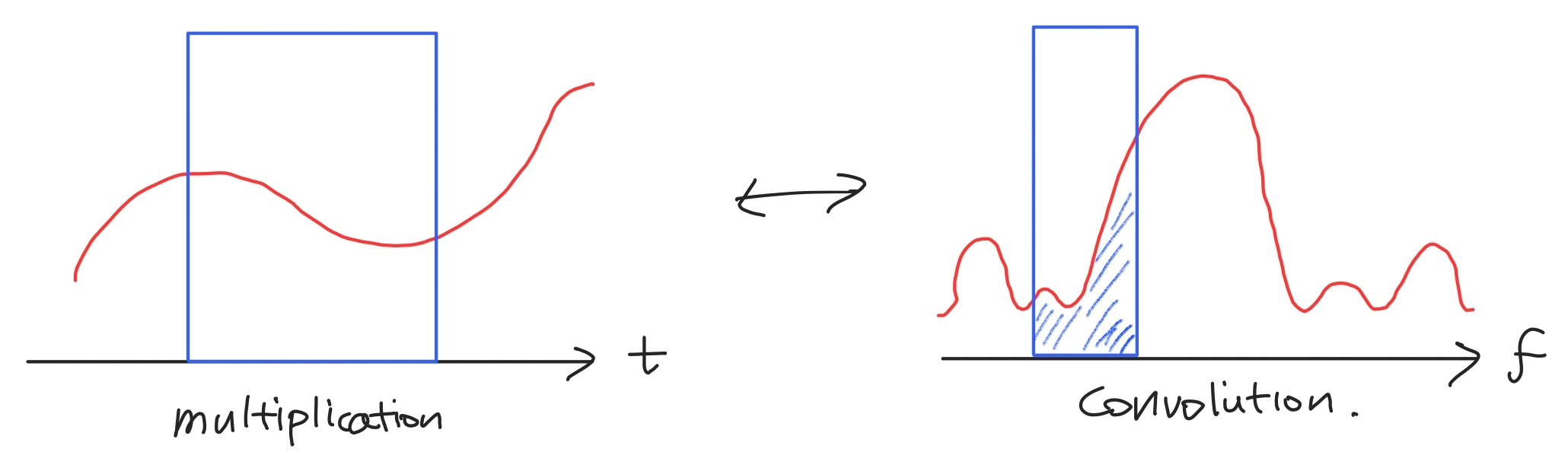
여기서 time resolution과 frequency resolution의 관계에 대해 생각해볼 수 있다.
window의 크기를 작게하면 우리는 시간축에 대해 세밀한 분석을 수행해줄 수 있지만, 주파수축에서는 convolution을 수행하는 band가 넓어지게 된다(wide band). 그러면 주파수축에 대해서는 오히려 resolution(분해능)이 떨어지게 된다.
예를 들어 아래와 같은 narrow band와 wide band가 있다고 가정을 해보자.

위에서의 해당 시간에 대한 신호의 frequency response가 아래와 같을 때,
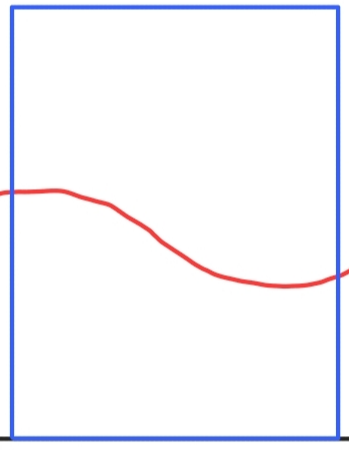

narrow band와 wide band에 대한 convolution 연산 결과는 다음과 같이 나타나게 된다.

즉 narrow band를 사용하면 frequency domain에서 각 frequency 에 대한 정보를 세밀하게 살릴 수 있게 된다.
아래는 실제 STFT 결과이다. 아래에서도 wide band를 사용했을 때는 time resolution이 좋고, frequency resolution이 떨어져 세로선의 형태가 나타나는 것을 확인할 수 있다. 반대로 narrow band를 사용했을 때는 time resolution이 떨어지고 frequency resolution이 좋아져 가로선의 형태가 나타나는 것을 확인할 수 있다.


| [LPC] Linear Predictive Analysis (0) | 2024.01.25 |
|---|---|
| [Cepstrum] Cepstrum과 Homomorphic analysis (0) | 2024.01.04 |
| [Window] Rectangular window와 Hamming Window (0) | 2023.11.09 |




| Rectangular window | Hamming window | |
 |
 |
|
| cutoff frequency |
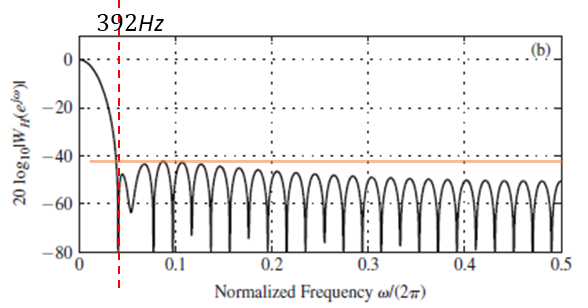
$$2\pi/L = 196Hz$$ | $$4\pi/L = 392Hz$$ |
| Attenuation | > 14 dB | > 40 dB |
같은 fram length를 가질 때, Hamming window의 cutoff frequency가 Rectangular window의 cutoff frequency의 두배이다. 즉 Hamming window(wide band)를 사용해 얻은 결과는 Rectangular window(narrow band)를 사용했을 때보다 frequency resolution이 떨어진다. (Rectangular window는 hamming window에 비해 freqeucncy resolution이 좋음)
하지만 Attenuation 같은 경우에는, Hamming window가 더 강하기 때문에 lobe가 약하게 나타난다. 그렇기 때문에 Rectangular window보다는 Hamming window를 사용했을 때, frequency band 외의 frequency가 연산에 개입이 적게 되기 때문에 error가 비교적 적다. (attenuation이 아주 강해서 lobe가 없는 경우가 noise가 없는 이상적인 상황)
즉, Rectangular window를 사용하면 frequency resolution이 좋다는 장점을 챙길 수 있으나 연산 과정에서 발생하게 되는 noise가 비교적 크고, Hamming window를 사용하면 frequency resolution은 떨어질 수 있으나 noise가 적다는 이점을 가진다.
| [LPC] Linear Predictive Analysis (0) | 2024.01.25 |
|---|---|
| [Cepstrum] Cepstrum과 Homomorphic analysis (0) | 2024.01.04 |
| [STFT] Frequency resolution과 Time resolution (3) | 2023.11.09 |
1. Visual Studio MFC 프로젝트 생성
[C++ 윈도우] 2019 비주얼스튜디오 MFC 프로젝트 만들고 간단하게 실행시켜보기 (대화상자 기반)
안녕하세요 양햄찌 블로그 주인장입니다. 맨날 콘솔에서 프로그래밍 할 수 없죠, C, C++, C#에는 콘솔 외에도 윈도우 앱을 만들 수 있는 환경을 제공하고 있는데, (저번 포스팅에서 말한적 있음!)
jhnyang.tistory.com
2. Form 스위칭
[MFC] Tab Control을 사용하지 않고 여러 Form 스위칭하기(예제 포함)
지난 포스팅에서 메인 다이얼로그에 새로운 다이얼로그를 붙이는 예제를 보여드렸었습니다. [MFC] Dialog에 Form(Dialog) 붙이기(예제 포함) [MFC] Dialog에 Form(Dialog) 붙이기(예제 포함) Dialog에 Dialog를 붙.
luckygg.tistory.com