Upsampling은 sampling rate을 높이는 것입니다. upsampling의 과정은 다음의 block diagram으로 나타낼 수 있습니다. (1) sampling rate을 L배로 높이고, (2) cutoff frequency가 $\pi/L$ 인 lowpass filter에 통과시켜줍니다.

두 가지 과정을 자세하게 정리해보도록 합시다.
1. Sampling rate expander
먼저 첫번째 ↑L 블럭을 sampling rate expander라고 합니다. 이 과정에서 우리는 L배로 sampling rate을 높이고자 할때 sample 사이에 L-1개의 0을 넣어 sampling의 수를 늘려줍니다.


2. Lowpass filter
그 다음 lowpass filter에 통과시켜주어야 합니다. 그렇지 않으면 time-aliasing이 발생할 수 있습니다. 그 이유를 아래 그림을 통해 알아보도록 하겠습니다.
아래는 upsampling 과정을 frequency domain에서 보여주는 그림입니다.
(a)는 아날로그 신호 x(t)의 CTFT 결과입니다. 이때 nyquist freqeuncy인 $\Omega_N$ 의 두 배로 sampling rate을 sampling 해주어 시퀀스 x[n]으로 나타내줍니다. 이 x[n]의 DTFT 결과는 (b)로 나타나게 됩니다.
이때 frequency 축이 $-\pi$ ~ $\pi$ 에 '$-\Omega_N$' ~ '$\Omega_N$' 값을 대입하여 normalize를 해준 것을 볼 수 있습니다.
(이에 대한 자세한 내용은 따로 포스팅을 하도록 하겠습니다.)
우리는 (1) 과정에서 time 축(사실상 sequence라 time은 아니지만)을 L배로 늘려서 scale을 시켜주었습니다. 그런데 frequency는 주기와 역수 관계이기 때문에 반대로 1/L 배로 줄어들게 됩니다. 만약 L = 2로 설정해주면 (b) 를 (c)와 같이 가로축을 scaling을 시켜준 것으로 나타낼 수 있습니다.
즉, (c)는 (1) Sampling rate expander 과정 직후의 결과입니다.


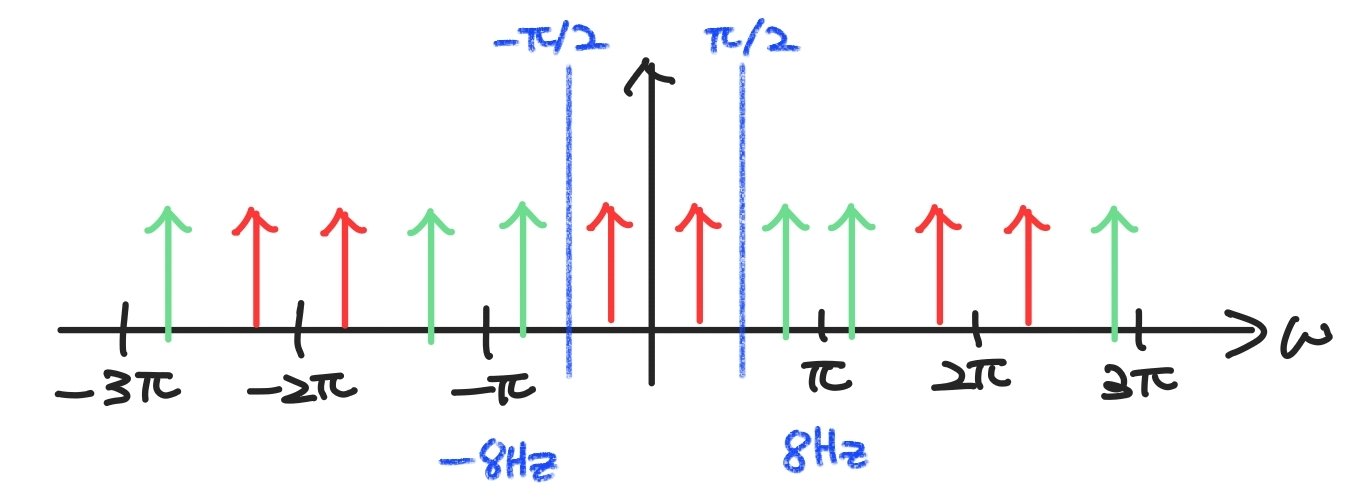
그런데 우리는 DTFT를 해줄 때, $-\pi$ ~ $\pi$ 에 sampling rate 값을 대입하여 줍니다. (c)를 다시보면 ' $\Omega_N$' ~ 2 '$\Omega_N$' 구간에 원래 존재하지 않던 고주파 성분들이 생긴 것을 볼 수 있습니다. 이것이 왜 문제가 되는지 간단한 예시를 통해 설명해드리겠습니다.
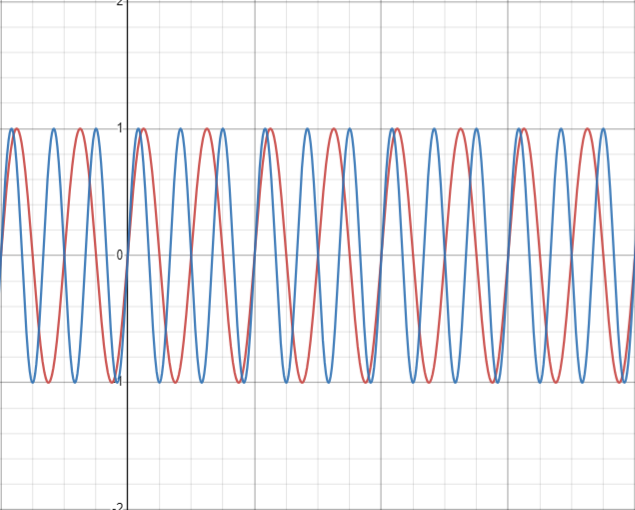
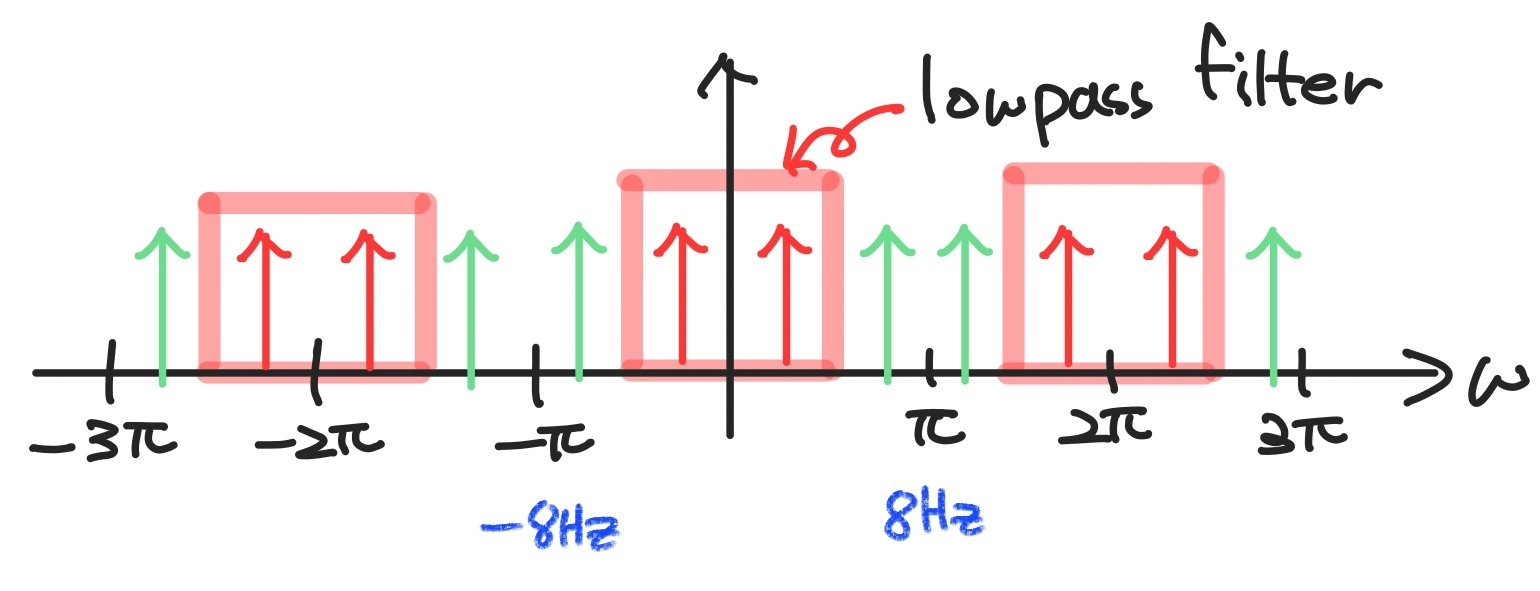
본래의 신호가 아래의 frequency가 2Hz인 빨간색의 신호가 있다고 생각해보겠습니다. 이 신호를 DTFT한 결과는 오른쪽과 같이 나타납니다. (samling rate = 8Hz라 가정)


이 신호의 sampling rate을 두 배로 늘려 16Hz로 upsamling을 하면, sampling rate expander 과정 이후 다음과 같이 변하게 됩니다. (위의 그림으로는 (c))
원래는 없던 초록색의 주파수 성분이 새로 생겨난 것을 볼 수 있습니다. 신호에 6Hz 성분이 생겨버렸습니다.
이것을 time domain에서 보면 아래와 같이 본래 신호와 달라진 것을 볼 수 있습니다. (c)
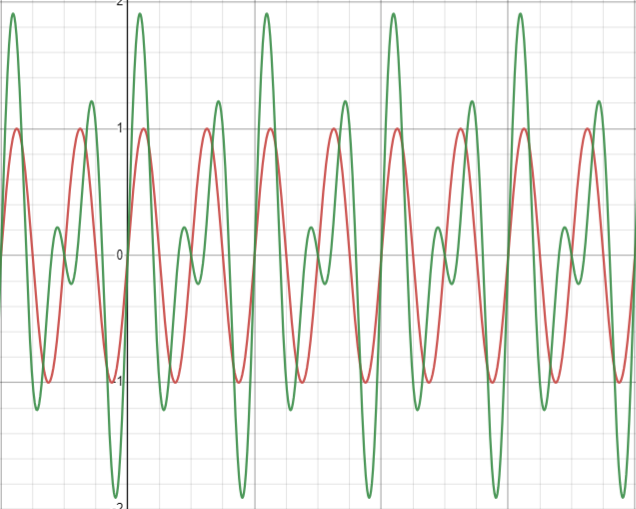
그렇기 때문에 우리는 아래와 같이 본래의 신호의 frequency 구간만 남기도록 cutoff frequency가 $\pi / L$ 인 lowpass filter (d)에 통과시켜주어야 우리가 원하는 upsamling과정이 끝나게 됩니다. (e)
'신호처리' 카테고리의 다른 글
| 윈도우에서 AWS 설치 및 데이터셋 다운로드 (1) | 2024.12.13 |
|---|---|
| [DSP] CTFT와 DTFT의 관계 (0) | 2024.01.04 |
| [Emphasis] Pre-emphasis 와 De-emphasis (0) | 2023.11.10 |
| Noise Pattern (0) | 2023.11.10 |