[STFT] Frequency resolution과 Time resolution

STFT는 특정 짧은 시간 구간을 windowing을 통해 추출해내고 해당 구간 동안에 DFT를 하여 연산을 수행한다.

이때 windowing은 signal을 window와 time domain에서 multiplication을 시키는 과정이다. time domain에서의 multiplication 연산은 frequency domain에서는 convolution 연산과 같다.

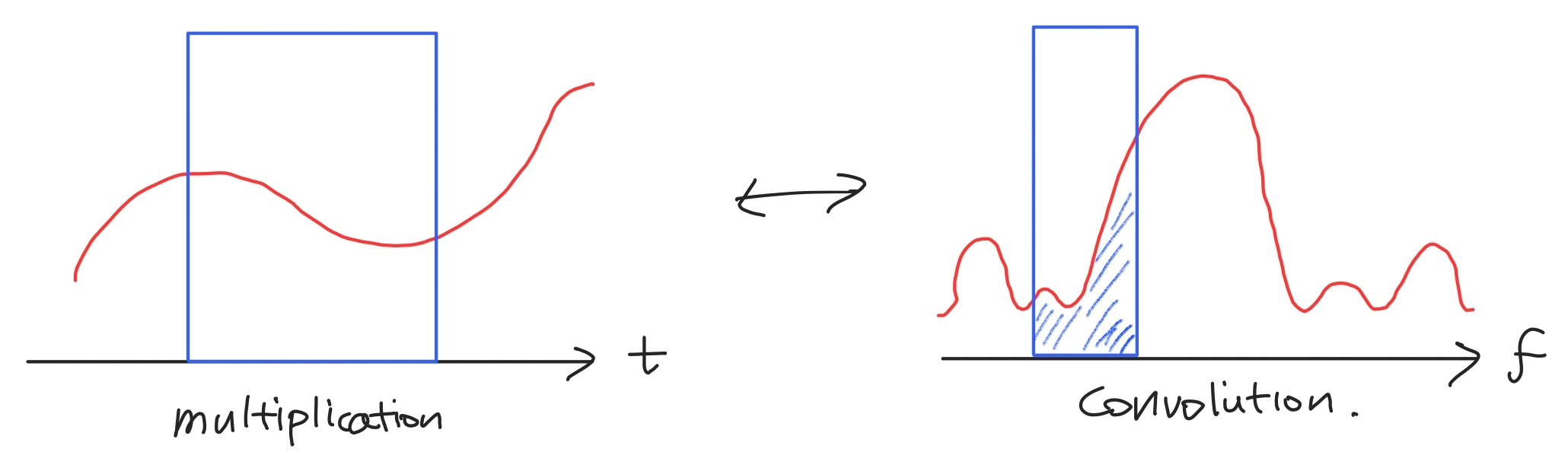
여기서 time resolution과 frequency resolution의 관계에 대해 생각해볼 수 있다.

window의 크기를 작게하면 우리는 시간축에 대해 세밀한 분석을 수행해줄 수 있지만, 주파수축에서는 convolution을 수행하는 band가 넓어지게 된다(wide band). 그러면 주파수축에 대해서는 오히려 resolution(분해능)이 떨어지게 된다.

 

예를 들어 아래와 같은 narrow band와 wide band가 있다고 가정을 해보자.

0

위에서의 해당 시간에 대한 신호의 frequency response가 아래와 같을 때,

time domain에서 window를 수행한 결과(왼)와 해당 signal의 frequency response

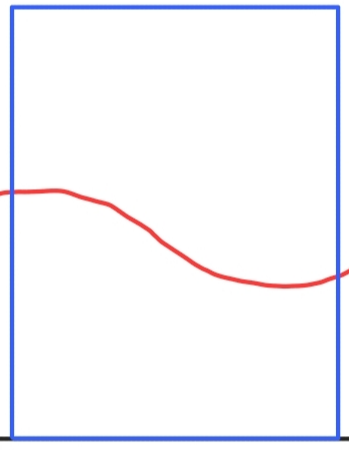
narrow band와 wide band에 대한 convolution 연산 결과는 다음과 같이 나타나게 된다.

대충 그려서 그림이 부정확할 수 있어요....

즉 narrow band를 사용하면 frequency domain에서 각 frequency 에 대한 정보를 세밀하게 살릴 수 있게 된다.

 

아래는 실제 STFT 결과이다. 아래에서도  wide band를 사용했을 때는 time resolution이 좋고, frequency resolution이 떨어져 세로선의 형태가 나타나는 것을 확인할 수 있다. 반대로 narrow band를 사용했을 때는 time resolution이 떨어지고 frequency resolution이 좋아져 가로선의 형태가 나타나는 것을 확인할 수 있다.

Wide band

Narrow band